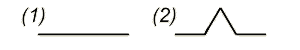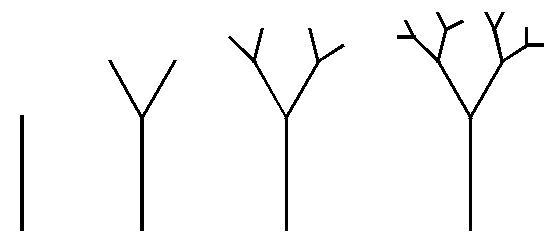Mini Projet Mathématiques Discrètes
ESSI 1
Courbes récursives
Vous devez rendre ce projet au plus tard le Vendredi 9 Janvier 18h. Au delà
le répertoire de rendu est fermé. Rien ne vous interdit de rendre
avant.
Les noms des fichiers qui vous sont donnés ici doivent être impérativement
respectés.
Le protocole de rendu
de projet est habituel.
Le newsgroup essi.essi1.projets est là pour que vous y posiez vos questions
concernant ce projet. Rien que vos questions concernant ce projet. Aucune réponse
ne sera faite à des questions posées par mail, afin que tous les
étudiants bénéficient des mêmes renseignements.
Vous devez travailler en binome : votre binome doit être dans le même
groupe de TD que vous. Si le groupe de TD comporte un nombre impair d'étudiants,
il doit y avoir au choix un monome ou un trinome. Les binomes doivent être
différents de ceux des mini projets précédents.
Remarque : Vous serez noté sur vos réponses
aux questions posées, et non sur d'éventuels enjolivements.
Le but de ce projet est d'étudier et de dessiner certaines courbes récursives.
Ces familles sont définies par
- une courbe initiale C1
- une règle de transformation qui permet de définit C k+1
en fonction de Ck
I- Première famille Pk :
Courbe initiale : P1: Un segment défini par les coordonnées
de ses deux extrémités. Ces extrémités sont aussi
appelées sommets (en rouge sur les dessins ci dessous) de P1.
Règle de transformation : On obtient Pk+1à partir
de Pk en remplaçant chaque segment s de longueur l reliant
deux sommets de Pk par une croix formée de l'intersection
de deux segments de droites, dont l'un est le segment s, et l'autre un segment
perpendiculaire à s de longueur l/2 ayant le même milieu
que s. Les sommets de Pk+1 sont les extrémités et les
centres de ces croix.
Voici P1,P2 et P3

Les points rouges matérialisent les sommets et sont là uniquement
pour une meilleure compréhension du texte. Ils ne font pas partie des
Pk et ne doivent pas être dessinés.
On peut voir ces courbes comme des arbres dont les sommets ont déjà
été définis et les arêtes sont les segments. Rappelons
qu'une feuille est un sommet de degré un.
- Etablir et résoudre une relation de récurrence permettant
de déterminer la longueur d'une telle courbe (la longueur étant
la somme des longueurs des segments de droites qui constituent le dessin),
en fonction de longueur du segment initial et de k.
- Etablir et résoudre des relations de récurrences sur le nombre
de sommets intérieurs (sommet qui n'est pas une feuille) , de feuilles
et d'arêtes.
- Ecrire une méthode récursive pour dessiner Pk..
Pour cela, créer une classe PkSol qui étend la classe (abstraite)Pk
(fichier Pk.java), en implémentant
la méthode drawPk. Vous ne devez en aucun cas modifier la classe Pk.
Un fichier TestPk.java vous est donné
pour tester votre implémentation. Pour dessiner, vous allez utiliser
uniquement la méthode Graphics.drawLine( int x1, int y1, int x2, int
y2), qui trace un segment de droite entre les deux points de coordonnées
(x1,y1) et (x2,y2). Rappelons que le point (0,0) est celui qui est en haut
et à gauche, et non pas en bas à gauche comme on en a l'habitude
en mathématiques. Voici par exemple, comment dessiner
un rectangle .
- Déterminer la complexité de votre méthode drawPk. Pour
vos calcul de complexité, vous supposerez que la méthode drawLine
est exécutée en temps constant.
- Mêmes questions pour une variante dont voici les premiers exemplaires
de la famille :
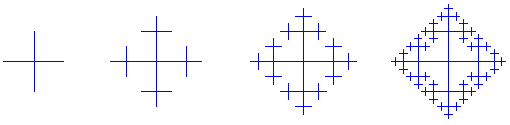
A RENDRE |
- Les réponses aux questions 1,2,4 et 5.1,5.2,5.4 dans un fichier
LisezMoi
- Les Fichiers PkSol.java, PkVarianteSol.java (et PkVariante.java et
PkVarianteTest.java), les .class et les javadoc correspondants.
|
II- Deuxième famille Sk
Voici S1 : c'est un segment de droite dont on connaît l'origine,
la longueur et l'inclinaison par rapport à l'horizontale 
La règle de transformation consiste à remplacer chaque  par
par  en respectant l'orientation
en respectant l'orientation
Voici donc S3 : 
- Poser et résoudre l'équation de récurrence qui permet
de calculer la longueur de Sk, en fonction de la longueur de S1.
La longueur d'une courbe étant la somme des longueurs des segments
qui la compose.
- Poser et résoudre l'équation de récurrence qui permet
de calculer le nombre de virages à gauche, et de virages à droite
dansSk
- Ecrire une méthode récursive pour dessiner Sk..
- Déterminer la complexité de votre méthode de dessin.
A RENDRE |
- Les réponses aux questions 1,2,4 dans le fichier LisezMoi
- Les fichiers Sk.java, SkTest.java et SkSol.java, les .class et les
javadoc correspondants.
|
III- Troisième famille: Kk
Cette fois ci le remplacement à chaque étape est le suivant :
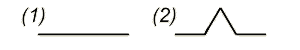
Et le dessin initial est un triangle équilatéral, voici donc
les trois premiers dessins de la famille

Questions
- Etablir et résoudre une relation de récurrence permettant
de déterminer la longueur d'une telle courbe (la longueur étant
la somme des longueurs des segments de droites qui constituent le dessin),
en fonction de longueur du triangle initial.
- Ecrire une méthode récursive pour dessiner Kk..
- Déterminer la complexité de votre méthode de dessin.
A RENDRE |
- Les réponses aux questions 1et 3 dans le fichier LisezMoi
- Les fichiers Kk.java, KkTest.java et KkSol.java, les .class et les
javadoc correspondants.
|
IV- Quatrième famille : dessin d' arbres Tk
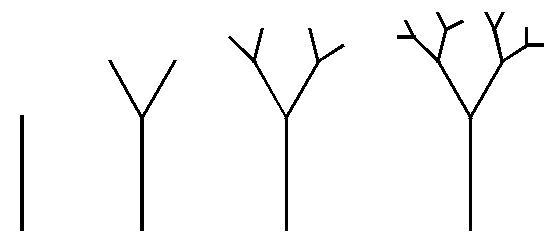
Cette fois-ci le principe est un peu différent : pour passer de l'arbre
p-aire à l'ordre k à l'arbre p-aire à l'ordre k+1, on ajoute
p (p=2 sur le dessin ci-dessus) nouvelles branches, plus courtes ( longueur
divisée par deux ) au niveau des feuilles de Tk, selon un
angle a calculer pour optimiser le dessin.
- Ecrire une méthode récursive pour dessiner les Tk. Déterminer
la complexité de cette méthode. Temporisez votre méthode,
pour pouvoir voir que le dessin de l'arbre se fait branche après branche
(vous trouverez un exemple de temporisation ici)
- Ecrire une méthode non récursive pour dessiner l'arbre.Pour
cette méthode utiliser une file. Cette méthode devra dessiner
l'arbre couche par couche, les feuilles sont donc dessinées en dernier.
Déterminer la complexité de cette nouvelle méthode.
- Pour obtenir des dessins qui ressemblent plus à des arbres tels que
ceux rencontrés dans la nature, il suffit d'ajouter un peu d'aléatoire:
le nombre de nouvelles branches peut par exemple être tiré aléatoirement
entre 1 max et l'angle de branchement peut lui aussi être aléatoire.
Ecrire une méthode récursive pour dessiner les Arbres aléatoires,
complexité ? Ci dessous deux exemples de tels arbres aléatoires.


A RENDRE |
- Les compléxités dans le fichier LisezMoi
- Les fichiers Tk.java, TkTest.java et TkSol.java, les .class et les
javadoc correspondants.
- Les fichiers TAleatoire.java, TAleatoireSol.java, TestTAleatoire.java,
les .class et javadoc correspondants.
|

Cette image est là pour montrer ce que l'on peut arriver à faire
avec la même idée, mais plus de travail !!



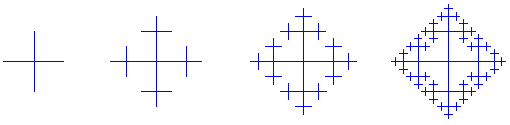
![]()
![]() par
par ![]() en respectant l'orientation
en respectant l'orientation![]()