Mathématiques Discrètes

ESSI 1

Bref corrigé de l’examen de Janvier 2002

 

 

Exercice 1

Un peu d’induction

On défini l’ensemble des arbres binaires de recherche de nombres comme suit :

Base : l’arbre binaire réduit à un seul nœud contenant un entier quelconque est un élément de ABR

Règles

                R1 :Si T est dans ABR et si n est un entier plus grand que tous les nombres contenus dans T, alors l’arbre binaire de racine un nœud contenant n, de sous arbre gauche T et de sous arbre droit vide est dans ABR

                R2 : Si T est dans ABR et si n est un entier plus petit que tous les nombres contenus dans T, alors l’arbre binaire de racine un nœud contenant n, de sous arbre gauche vide  et de sous arbre droit T est dans ABR

R3 : Si T et T’  sont  dans ABR et si n est un entier plus grand que tous les nombres contenus dans Tet plus petit que tous les nombres contenus dans T’, alors l’arbre binaire de racine un nœud contenant n, de sous arbre gauche T et de sous arbre droit T’ est dans ABR

 

1-                         Si on utilise uniquement les nombres 1,2,3 et 4, combien y a-t-il d’arbres binaires de recherche de nombres ayant 4 sommets

On peut les énumérer tous, mais alors on risque d’en oublier. Le mieux c’est de dire : soit c_n le nombre d’ABR ayant n sommets et contenant les nombres de 1 à n. On a

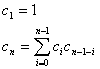                 à condition de poser c₀=1.

On reconnaît là l’équation des  nombres de catalans et l’on trouve c₄=14.

Ou bien on utilise cette équation pour calculer c₂, c₃ et c₄, et l’on trouve c₂=1+1=2, c₃3=2+1+2=5 et c₄=5+2+2+4=14

 

                2. Soit A dans ABR définir inductivement une fonction qui teste si n est contenu dans A. Essayez d’écrire une fonction dont la complexité soit la meilleure possible. Prouvez votre fonction

 

               

                Appelons appartient la fonction de NxABR dans {vrai,faux} , telle que appartient(n,A) est vrai si et seulement si n est contenu dans A.

 

Notons A(n) l’ABR réduit à un seul nœud contenant l’entier n, A(T,n), R1(T,n) l’ABR construit par la règle R1, R1(T,n) l’ABR construit par la règle R2, R3(T,T’,n) l’ABR construit par la règle R31,

 

 

 

Soit App la fonction de NxABR dans {vrai,faux} définie inductivement par

                App(n,A(m))=(n=m)

                App(n,R1(T,m))=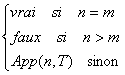

App(n,R2(T,m))=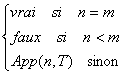

App(n,R3(T,T’,m))=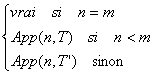

 

On montre facilement par induction structurelle que App et Appartient sont égaux.

 

 

On demandait une fonction dont la complexité soit la meilleure possible. Pour véritablement parler de la complexité il faudrait programmer ces fonctions et regarder le coût des primitives qui permettent de « découper » un ABR  en ses sous-arbres gauches et droits. Avant cela tout ce que l’on peut dire c’est que si l’on programme récursivement en suivant cette définition inductive le calcul de App(n,T) induira un nombre d’appels récursifs en Omega(hauteur(T)). 

 

 

 

 

Exercice 2  Tour de Hanoï

 

On considère une variante des tours de Hanoï avec trois piquets 1,B,C et n disques.

-          les n disques sont de taille différente

-          initialement les n disques sont rangés sur le piquet A, du plus grand en bas, au plus petit en haut

-          on désire amener les n disques dans le même ordre sur le piquet C

-          on ne peut déplacer qu’un seul disque à la fois

-          on ne peut pas poser un disque sur un disque de taille inférieure

-          tous les mouvements de disques doivent se faire via le piquet centrql (un déplacement direct de A vers C ou de C vers A est interdit

 

1.       Déterminer et prouver l’équation de récurrence correspondant au nombre minimum de déplacements de disques

 

Commençons par donner un algorithme récursif A(n,A,C) pour déplacer les n disques de A vers C :

Si n=0, ne rien faire,

Sinon :

- A(n-1,A,C)

                - déplacer le grand disque de A vers B

                -A(n-1,C,A)

                - déplacer le grand disque de B vers C

                -A(n-1,A,C)

 

A et C jouant des rôles identiques le nombre de mouvements minimum pour déplacer n tours de A vers C ou de C vers A  est le même. Soit m_n ce nombre, on a

-m₀=0

-m_n<=3m _n-1+2

 

Montrons que cette inégalité est en fait une égalité (ce que vous avez quasiment tous oublié de faire)

Tout algorithme réalisant le déplacement des n disques de A vers C devra déplacer le grand disque de A vers C, comme le déplacement  ne peut se faire directement, il y aura forcement un premier déplacement du grand disque de A vers B, pour que ce déplacement puisse se faire il aura auparavant fallu déplacer les n-1 autres disques de A vers C, en observant toutes les contraintes.  Il faudra aussi apporter le grand disque de B sur C, entre temps  les n-1 disques qui étaient sur C ont du retourner sur A, etc….

 

Au final on a donc l’équation

-m₀=0

-m_n=3m _n-1+2

 

 

2.       Résoudre cette équation

 

C’est une équation  de récurrence linéaire non homogène d’ordre 1.

Les solutions de l’équation homogène associée m_n=3m _n-1, sont de la forme m_n=a.3ⁿ

 La seule racine du polynôme caractéristique étant 3 (et non 1), on cherche une solution particulière sous forme de constante et l’on trouve m_n=-1

Les solutions générales de l’équation non homogène sont donc de la forme m_n=a.3ⁿ-1.

On a donc m_n=3ⁿ-1, puisque m₀=0

 

Exercice 3  Un exercice sur les graphes

Le complémentaire d’un graphe non orienté G=(V,E) est le graphe =(V, ) tel qu’il existe une arête entre x et y dans si et seulement si il n’y a pas d’arête entre x et y dans G.

 

                1 Montrer que si G n’est pas connexe alors l’est.

 

Soient x et y deux sommets quelconques de V.

Nous allons montrer qu’il y a toujours une chaîne entre x et y dans .

 

 Si x et y ne sont pas reliés par une arête dans G, alors ils le sont dans et ils sont donc reliés par une chaîne dans .

 Si x et y sont reliés par une arête dans G, alors ils sont dans la même composante connexe de G. G n’étant pas connexe, il existe au moins une autre composante connexe. Soit z un sommet de G n’étant pas dans la même composante connexe que y et z. x et z d’une part et y et z d’autre part n’étant pas reliés  par une arête dans G, alors ils le sont sont dans et donc x et y sont  reliés par une chaîne dans .

Remarque : on a en fait montré quea un diamètre inférieur ou égal à deux.

 

On pouvait aussi faire une démonstration par récurrence, certains l’ont fait juste, d’autres l’ont fait fausse…….

 

2         La réciproque est elle vraie ?

 

Non, par exemple le graphe égal à une chaîne de longueur 3 (4 sommets)  est connexe et son complémentaire aussi  (ce complémentaire étant lui aussi une chaîne de longueur 3).

 

3         On dit que deux graphes G1 et G2 d’ordre n sont isomorphes si et seulement si ils sont égaux à la numérotation des sommets près. Montrer que si un graphe G est auto-complémentaire (c'est-à-dire isomorphe à son complémentaire) alors le nombre de sommets de G est soit un multiple de 4 soit un multiple de 4 plus un.

 

Si un graphe est isomorphe a son complémentaire, il a autant d’arêtes que lui. Or la somme du nombre d’arête d’un graphe d’ordre n  et du nombre d’arête de son complémentaire est égal à n(n-1)/2. Un graphe auto-complémentaire d’ordre n a donc n(n-1)/4 arêtes. Ce nombre est entier, comme 2 ne peut diviser n et n-1 en même temps, 4 doit diviser n ou n-1.

 

4         Trouver les deux plus petits graphes qui sont auto-complémentaires

 

Pour n=0, le graphe vide

Pour n=1 le graphe réduit à un sommet

Mais ces deux là sont un peu « pathologiques » , alors allons voir plus loin

Pour n=4 la chaîne de longueur 3

Pour n=5 le cycle de longueur 5 (il y a aussi un autre exemple pour n=5)