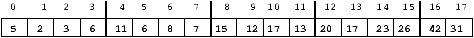Les méthodes de tous les exercices doivent être écrites
dans les classes fournies en annexe.
EXERCICE 1
On considère les tas décroissants (resp. croissants) étudiés en
cours.
Ecrivez intégralement la classe TasDecroissant (resp. TasCroissant), classe dont les instances sont les tas vus en cours.
Ecrivez la classe TriTas qui implémente le tri par tas vu en cours.
EXERCICE 2
On considère un tas (croissant ou décroissant) ne contenant que des
objets de clefs distinctes. On désire pouvoir supprimer un
élément de clef donnée dans un tel tas tout en conservant au tas sa
propriété de tas.
Ecrivez la méthode publique extraire(int k) de la classe TasDecroissant (resp. TasCroissant), méthode qui supprime
l'élément de clef k dans un tas décroissant (resp. croissant).
Que pensez-vous de la méthode précédente si maintenant on désire
supprimer tous les éléments d'une clef donnée dans un tas pouvant
contenir plusieurs éléments de même clef ?
EXERCICE 3
Un tas (croissant ou décroisssant) d-aire (d > 1) est un tas
représenté par un arbre parfait d-aire, c'est à dire un arbre
parfait dont les noeuds ont au plus d fils. A la manière des arbres
parfaits binaires (d = 2), un arbre parfait d-aire peut
être représenté par un tableau,
Expliquez comment on peut représenter un arbre parfait d-aire à
l'aide d'un tableau et donnez le numérotage des noeuds en fonction de
d.
Calculez la hauteur d'un tas d-aire de n éléments en
fonction de n et de d et donnez la complexité des méthodes
appliquées sur ce tas.
En vous inspirant largement de la classe TasDecroissant, écrivez la
classe TasDaireDecroissant (resp. TasDaireCroissant) qui
implémente les tas d-aire.
EXERCICE 4
On veut écrire une version du tri rapide basée sur une
méthode de partitionnement qui partitionne une tranche de tableau en trois parties (et non deux parties comme la méthode étudiée en
cours). Le comportement de la nouvelle méthode partitionnerEnTrois de
la classe PartitionTernaire est le suivant : étant
donné un tableau T et deux indices i et j tels ques i < j, partitionner(i,j) déplace éventuellement des objets dans
T et retourne deux indices g et d (sous la forme d'un
tableau P à deux éléments avec P[0] = g et P[1] =
d) tels que g < d, et qui partagent la tranche T[i..j] en
trois parties comme suit :
avec T[g] £ T[d],
et " x
Î T[i..g-1], " y Î T[g+1..d-1], "
z Î T[d+1..j], on a :
x < T[g], T[g] £ y, y < T[d] et T[d]
£ z
où x < y signifie x.clef() < y.clef() si x et y
sont deux objets à clef.
En utilisant la méthode partitionnerEnTrois de la classe PartitionTernaire, écrivez les méthodes trier de la classe TriRapideTernaire, telles que t.trier() trie le tableau contenu dans
l'objet t en place par la méthode du tri rapide.
Que pensez-vous de la complexité de la méthode trier de la classe TriRapideTernaire par rapport à celle de la méthode trier étudiée en
cours ?
En utilisant la méthode partitionner de la classe PartitionTernaire (la méthode étudiée en cours), écrivez le corps de la
méthode partitionnerEnTrois de la classe PartitionTernaire.
En vous inspirant de la méthode partitionner, réécrivez le corps de
la méthode partitionnerEnTrois de la classe PartitionTernaire.
EXERCICE 5
On dit qu'un tableau est presque triée à l'ordre k (k
³ 1) si, en le découpant suivant les indices multiples de k,
les tranches ainsi obtenues sont globalement triées par ordre
croissant. Par exemple, considérons le tableau suivant (seules les clefs
des éléments apparaissent) :
Il est presque trié à l'ordre 4, car si on considère les tranches de
longueur 4 (sauf peut-être la dernière de longueur inférieure ou
égale à 4), elles sont globalement ordonnées (i.e. si on considère
deux tranches consécutives, un élément quelconque de la première est
inférieur ou égal à un élément quelconque de la deuxième).
Ecrivez la méthode publique presqueTrie de la classe PresqueTrier telle que t.presqueTrie(k) (avec k ³ 1) retourne
true si le tableau contenu dans l'objet t est presque triée à
l'ordre k.
Soient i et j deux entiers tels que i < j, et un
entier k, k ³ 1. Ecrivez la méthode privée estInclus de la
classe PresqueTrier telle que estInclus(i,j,k) teste si
l'intervalle [i,j] (i £ j) est inclus dans un intervalle [a,b[ où
a et b sont deux multiples de k consécutifs (par exemple, estInclus(13,15,4) retourne true car [13,15] Í [12,16[, et
12 et 16 sont deux multiples de 4 consécutifs).
Ecrivez la méthode presqueTrier de la classe PresqueTrier telle
que l'exécution de t.PresqueTrier(k) (k ³ 1), réarrange le
tableau contenu dans l'objet t de façon à ce qu'il soit presque
trié à l'ordre k.
EXERCICE 6
On désire implémenter la méthode de tri par fusion. Comme le tri
rapide, cette méthode utilise la technique ``diviser pour régner''
pour effectuer un tri avec une complexité en Q(n lg(n)) où n est
la taille du tableau à trier. L'inconvénient de cette méthode est
qu'elle nécessite l'utilisation d'un tableau temporaire de la taille du
tableau à trier.
Ecrivez toutes les méthodes de la classe TriFusion de manière que
t.trier() trie le tableau contenu dans l'objet t avec une
complexité de Q(n lg(n)) où n est la taille de ce tableau.
EXERCICE 7
La partie délicate du tri rapide est la méthode de
partition. L'écriture de cette méthode est plus simple si on dispose d'un
tableau temporaire en plus du tableau à trier. Le tri n'est alors plus en
place, mais conserve néanmoins sa bonne complexité.
Ecrivez la méthode partionnerDans de la classe TriRapideNEP
telle que partitionnerDans(A,B,i,j) partitionne la tranche de tableau
A[i..j] dans la tranche de tableau B[i..j] et retourne l'indice
du pivot.
En définissant autant de méthodes privées que nécessaire, écrivez
la méthode trier de la classe TriRapideNEP telle que t.trier() trier le tableau contenu dans l'objet t par la méthode du
tri rapide en utilisant un tableau temporaire.
EXERCICE 8
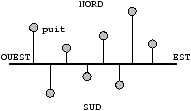
Une compagnie pétrolière projette de construire un oléoduc d'Est en
Ouest à travers un champ pétrolier contenant n puits de
pétrole. Chaque puits doit être raccordé à l'oléoduc principal à
l'aide d'un petit oléoduc orienté Nord-Sud, perpendiculaire à
l'oléoduc principal. On connaît les coordonnées de chaque puits dans
un repère cartésien d'abscisse Est-Ouest et d'ordonnée Nord-Sud et
chaque puits a une abscisse et une ordonnée unique. On cherche l'emplacement
de l'oléoduc principal (une droite) qui minimise la longueur totale
des raccordements :
En supposant que deux puits distincts ont leurs coordonnées deux à deux
distinctes, expliquez comment cet emplacement peut être calculé en
O(n).
EXERCICE 9
On désire écrire une version du calcul d'un rang statistique à l'aide de la
méthode de partition élaborée à l'exercice 4.
En utilisant la méthode partitionnerEnTrois de l'exerice 4, écrivez
la méthode rang de la classe RangEnTrois, telle que r.rang(k) retourne le k-ième rang statistique du tableau contenu
dans r.
This document was translated from LATEX by
HEVEA.