TD 6 : Arbres de recherche
Les méthodes de tous les exercices doivent être écrites
dans les classes fournies en annexe.
EXERCICE 1
Ce premier exercice sur les arbres de recherche consiste à écrire
intégralement la classe ABR présentée en cours.
Complétez la classe ABR fournie en annexe et écrivez toutes les
méthodes publiques.
EXERCICE 2
Etant donné un arbre binaire de recherche, on cherche à supprimer
de l'arbre tous les éléments de clef strictement inférieure
(resp. strictement supérieure) à une valeur donnée.
Ecrivez les méthodes elaguerInferieur(int k) et
elaguerSuperieur(int k) de la classe ABR telles que elaguerInferieur(k) (resp. elaguerSuperieur(k)) supprime tous les
éléments de l'arbre de clef strictement inférieure (resp. strictement
supérieure) à k.
EXERCICE 3
Etant donné un arbre binaire de recherche, on veut construire un tableau
trié strictement croissant contenant exactement les élément de
l'arbre. Inversement, étant un tableau trié strictement croissant, on
veut construire un arbre binaire de recherche contenant exactement tous les
éléments de l'arbre.
Ecrivez la méthode tableau() de la classe ABR telle que A.tableau() retourne un tableau trié croissant contenant exactement les
éléments de l'arbre A.
Ajouter le constructeur ABR(ObjetAClef[] T) à la classe ABR,
constructeur qui, étant donné T un tableau trié croissant,
construit un arbre binaire de recherche contenant exactement les éléments
du tableau T.
EXERCICE 4
Un Arbre Binaire de Recherche à Occurences (ou ABRO dans la
suite) est un arbre binaire de recherche pouvant contenir plusieurs objets
à clef distincts de même clef. Un ABRO est une instance de la
classe ABRO donnée en annexe. Etant donné un ABRO A, les
différents objets à clef de A de clef k s'appellent les occurences de k dans A. Les occurences d'une clef donnée sont
implicitement ordonnées suivant l'ordre dans lequel on a ajouté les
objets à clef correspondants dans l'arbre. Ainsi, la première occurence
de clef k dans A est l'objet à clef ajouté en premier dans A parmi
tous les objets à clef de clef k de A. Plus généralement, la
ième occurence de clef k dans A est le
ième objet à clef ajouté dans A parmi tous les objets
à clef de clef k de A. Quand on ajoute un objet à clef x de clef
k dans un ABRO A dont la racine est un objet à clef y de clef
k, x est ajouté dans le sous-arbre gauche de A. Par exemple,
l'adjonction successive des objets à clef tous distincts
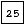 , 13,
, 13,
 , 11,
, 11,
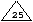 , 27, 37,
, 27, 37,
 , 29, 28,
, 29, 28,
 , 20,
, 20,
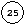 et 17 dans un ABRO
initialement vide donne l'ABRO suivant :
et 17 dans un ABRO
initialement vide donne l'ABRO suivant :
Dans l'arbre ci-dessus, l'objet à clef
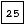 est la
première occurence de la clef 25, l'objet à clef
est la
première occurence de la clef 25, l'objet à clef
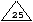 est la deuxième occurence
de la clef 25 et l'objet à clef
est la deuxième occurence
de la clef 25 et l'objet à clef
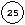 est la troisième occurence de
la clef 25 dans l'arbre. De même, les objets à clef
est la troisième occurence de
la clef 25 dans l'arbre. De même, les objets à clef
 ,
,
 et
et
 sont respectivement la
première, deuxième et troisième occurence de la clef 31 dans
l'arbre. Si on supprime de l'arbre la première occurence de la clef 25
(soit l'objet à clef
sont respectivement la
première, deuxième et troisième occurence de la clef 31 dans
l'arbre. Si on supprime de l'arbre la première occurence de la clef 25
(soit l'objet à clef
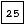 ) et la deuxième occurence de
la clef 31 (soit l'objet à clef
) et la deuxième occurence de
la clef 31 (soit l'objet à clef
 )
l'arbre devient :
)
l'arbre devient :
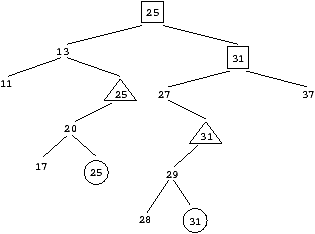
Maintenant, 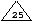 et
et
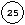 sont respectivement la
première et la deuxième occurence de la clef 25 dans l'arbre, et
sont respectivement la
première et la deuxième occurence de la clef 25 dans l'arbre, et
 et
et
 sont respectivement la
première et la deuxième occurence de la clef 31 dans l'arbre.
sont respectivement la
première et la deuxième occurence de la clef 31 dans l'arbre.
Ecrivez la méthode publique ajouter
de la classe ABRO telle que A.ajouter(x) ajoute à l'arbre
binaire de recherche à occurences A l'objet à clef x.
Ecrivez la méthode publique rechercher de la
classe ABRO telle que A.rechercher(k,i) retourne la
ième occurence de clef k de l'arbre A si elle
existe, null sinon.
En utilisant la méthode privée supprimerRacine de l'exercice 1, écrivez la méthode
publique supprimer de la classe ABRO telle que A.supprimer(k,i) supprime la ième occurence de clef k
dans l'arbre A si elle existe, ou ne fait rien sinon.
EXERCICE 5
La méthode d'adjonction d'un nouvel élément dans un arbre binaire de
recherche vue en cours place l'élément à ajouter sur une nouvelle
feuille de l'arbre. On veut écrire une nouvelle méthode d'adjonction
telle qu'après l'ajout, le nouvel élément soit la racine de l'arbre.
Ecrivez la méthode scinder dans la classe ABR telle qu'après
l'évaluation de scinder(A,k,G,D) où A est un arbre binaire de
recherche, k un entier (une clef) et G et D deux arbres
binaires de recherche vides on ait :
-
G contient tous les éléments de A' de clef inférieure
ou égale à k
- D contient tous les éléments de A' de clef strictement
supérieure à k
- A est vide
où A' est l'arbre A initial (avant l'appel de la méthode).
Ecrivez une nouvelle méthode ajouter dans la classe ABR qui
utilise la méthode précédente pour ajouter un nouvel élément à un
arbre binaire de recherche en le plaçant à la racine.
EXERCICE 6
La fusion de deux arbres binaires de recherche A et B est un arbre
binaire de recherche C tel que C contient tous les ObjetAClefs de
A et tous les ObjetAClefs de B, un arbre pouvant posséder deux
ObjetAClefs distincts ayant la même clef.
En utilisant la méthode de l'exercice précédent, écrivez la méthode fusionnerAvec dans classe ABR telle qu'après l'évaluation de
A.fusionnerAvec(B) on ait :
-
A contient tous les éléments de A' et tous les
éléments de B
- B est vide
où A' est l'arbre A initial (avant l'appel de la méthode).
EXERCICE 7
Dessinez un arbre AVL de hauteur 4 qui contient le plus d'éléments
possible et un arbre AVL de hauteur 4 qui contient le moins d'éléments
possible.
EXERCICE 8
Dessinez l'arbre AVL qu'on obtient si on ajoute successivement les entiers
9, 4, 1, 3, 2, 8, 10, 6, 5, 11 et 7 dans un arbre AVL initialement vide.
EXERCICE 9
Donnez l'ordre dans lequel il faut supprimer les éléments de l'arbre obtenu à
l'exercice précédent pour vider entièrement cet arbre sans provoquer aucune
rotation.
EXERCICE 10
Dessinez l'arbre AVL obtenu après la suppression succéssive des entiers
7, 8, 9, 11, 10, 4, 1 et 2 de l'arbre obtenu à l'exercice 8.
This document was translated from LATEX by
HEVEA.
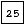 , 13,
, 13,
 , 11,
, 11,
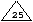 , 27, 37,
, 27, 37,
 , 29, 28,
, 29, 28,
 , 20,
, 20,
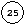 et 17 dans un ABRO
initialement vide donne l'ABRO suivant :
et 17 dans un ABRO
initialement vide donne l'ABRO suivant : 
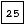 est la
première occurence de la clef 25, l'objet à clef
est la
première occurence de la clef 25, l'objet à clef
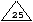 est la deuxième occurence
de la clef 25 et l'objet à clef
est la deuxième occurence
de la clef 25 et l'objet à clef
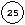 est la troisième occurence de
la clef 25 dans l'arbre. De même, les objets à clef
est la troisième occurence de
la clef 25 dans l'arbre. De même, les objets à clef
 ,
,
 et
et
 sont respectivement la
première, deuxième et troisième occurence de la clef 31 dans
l'arbre. Si on supprime de l'arbre la première occurence de la clef 25
(soit l'objet à clef
sont respectivement la
première, deuxième et troisième occurence de la clef 31 dans
l'arbre. Si on supprime de l'arbre la première occurence de la clef 25
(soit l'objet à clef
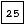 ) et la deuxième occurence de
la clef 31 (soit l'objet à clef
) et la deuxième occurence de
la clef 31 (soit l'objet à clef
 )
l'arbre devient :
)
l'arbre devient :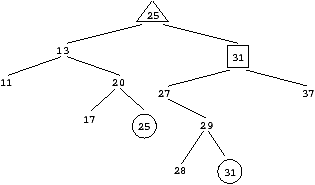
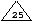 et
et
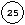 sont respectivement la
première et la deuxième occurence de la clef 25 dans l'arbre, et
sont respectivement la
première et la deuxième occurence de la clef 25 dans l'arbre, et
 et
et
 sont respectivement la
première et la deuxième occurence de la clef 31 dans l'arbre.
sont respectivement la
première et la deuxième occurence de la clef 31 dans l'arbre.